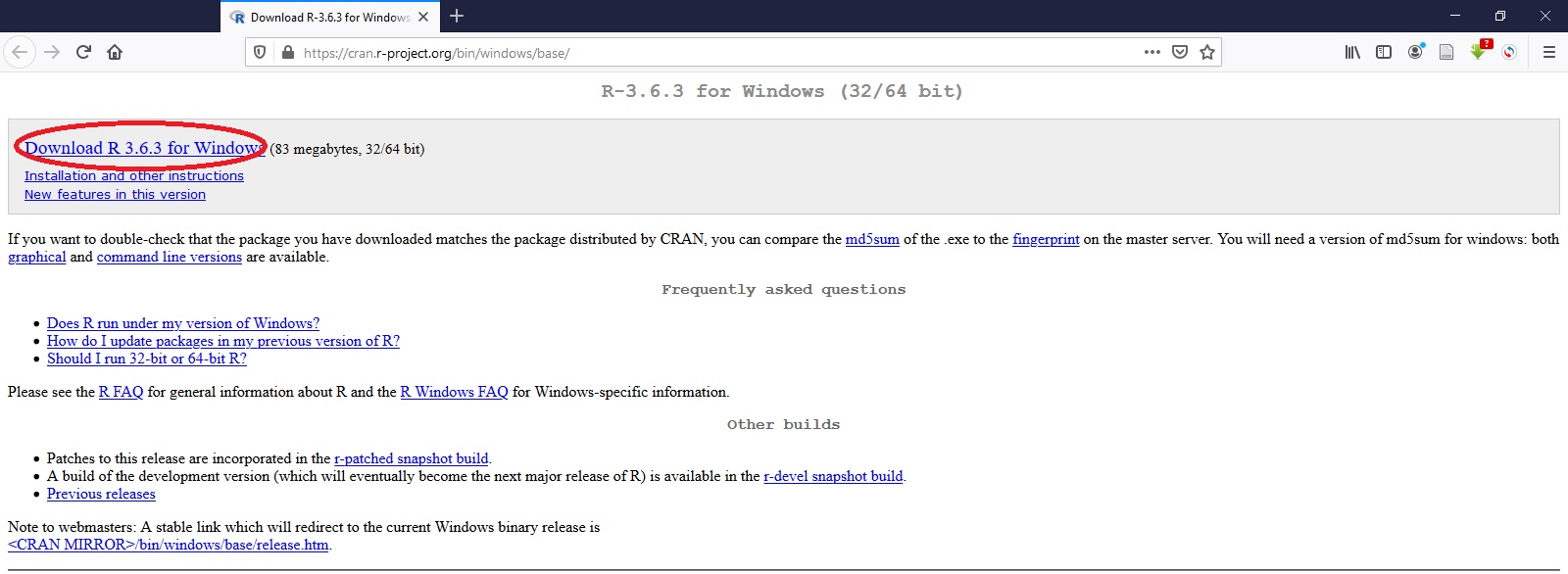
2.1Types élémentaires de R
• Numeric qui peut être entier (integer) ou double (double). Les opérateurs applicables
sont : + , - , * , / , ^ , %% (modulo) , %/% (division entière)
Exemple: 7 / 2 → 3.5 (division entre valeurs réelles) ; en revanche 7 %/% 2 → 3 (division
entière)
• Logical correspond au type booléen, il prend deux valeurs possibles TRUE et FALSE
(en majuscule) que l’on peut abréger avec T et F.
Les opérateurs sont :
! (signifie négation),
&& (signifie ET logique),
|| (signifie OU logique),
xor() (signifie OU exclusif)
Exemple: !T résultat = F
xor(T,F) résultat = T
T && F résultat = F ….etc.
• Character désigne les chaînes de caractères. Une constante chaîne de caractère
doit être délimitée par des guillemets (")
• Remarque : pour connaître la classe d’un objet (le type associé à un objet, on
utilise la fonction class(nom de l’objet)
Exemple : class(2020) résultat="numeric"
class("Bioinformatique ") résultat= "character"
2.2 Sous forme de vecteurs
L’unité de base en R est le vecteur.
vecteurA <-c(13,27,21,22,31,11,14,18,13,9,19,16) # “c” = fonction qui combine les arguments pour former un vecteur.
vecteurB <-c(11,12,11,13,9,17,15,22,24,13,13,15)
Notez : les données sont séparées par des virgules; les notations décimales se font “à l’anglaise”, par des points.
append (vecteurA, vecteurB) # Concatène les vecteurs = [1] 13 27 21 22 31 11 14 18 13 9 19 16 11 12 11 13 9 17 15 22 24 13 13 15
vecteurtotal <-c(append(vecteurA, vecteurB)) # Utilise append pour former un nouveau vecteur
vecteurtotal # le résultat= [1] 13 27 21 22 31 11 14 18 13 9 19 16 11 12 11 13 9 17 15 22 24 13 13 15
vecteursomme <-c(vecteurA + vecteurB) # Additionne les vecteurs terme à terme
vecteursomme # le résultat= [1] 24 39 32 35 40 28 29 40 37 22 32 31
La notation vectorielle peut aussi s’appliquer à des données catégorielles
lapins <-c("gris", "noires", "sauvages") # Mettre les noms entre guillemets dactylos et la commande names peut servir à utiliser ces données comme ”ètiquettes”
testlapins <-c (33, 40, 15)
names (lapins) <- testlapins
lapins
33 40 15
"gris" "noires" "sauvages"
Manipulation de vecteurs
#Génération de suites de nombres :
seq(1, 9, by = 2) # le résultat = [1] 1 3 5 7 9
#Pour générer la suite des nombres de 1 à la valeur de l’argument :
seq_len(10) # le résultat = [1] 1 2 3 4 5 6 7 8 9 10
#Répétition de valeurs ou de vecteurs :
rep(2, 10) # le résultat = [1] 2 2 2 2 2 2 2 2 2 2
#Tri en ordre croissant ou décroissant :
sort(c(4, -1, 2, 6)) # le résultat = [1] -1 2 4 6
#Rang des éléments d’un vecteur dans l’ordre croissant ou décroissant :
rank(c(4, -1, 2, 6)) # le résultat = [1] 3 1 2 4
#Ordre d’extraction des éléments d’un vecteur pour les placer en ordre croissant ou décroissant :
order(c(4, -1, 2, 6)) # le résultat = [1] 2 3 1 4
#Renverser un vecteur :
rev(1:10) # le résultat = [1] 10 9 8 7 6 5 4 3 2 1
#Premiers éléments d’un vecteur (n > 0) ou suppression des n derniers (n < 0) :
head(1:10, 3) # le résultat = [1] 1 2 3
head(1:10, -3) # le résultat = [1] 1 2 3 4 5 6 7
#Tail extraction des n derniers éléments d’un vecteur (n > 0) ou suppression des n premiers (n < 0) :
tail(1:10, 3) # le résultat = [1] 8 9 10
tail(1:10, -3) # le résultat = [1] 4 5 6 7 8 9 10
#Unique extraction des éléments différents d’un vecteur :
unique(c(2, 4, 2, 5, 9, 5, 0)) # le résultat = [1] 2 4 5 9 0
2.3 Sous forme de matrice 1:
matrice1 <-matrix (vecteurtotal, ncol = 2, byrow = F) # deux colonnes ; par ligne = FAUX
matrice1
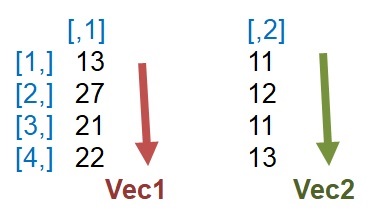
#notez les virgules dans les crochets ; [, n°colonne] ; [n°ligne ,]
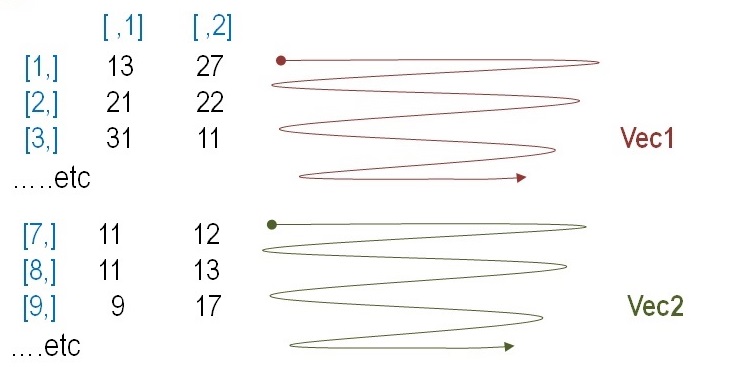
matrice2 <-matrix (vecteurtotal,ncol = 2, byrow = T) # deux colonnes ; par ligne = VRAI
matrice2
matricesomme <-matrix ((matrice1 + matrice2), ncol=2) ; matricesomme # le point virgule sépare deux commandes
[,1] [,2]
[1,] 26 38 (13 + 13) (11 + 27)
[2,] 48 34 (27 + 21) (12 + 22)
[3,] 52 22
….etc
Matricesommeligne1 <-matrix ((matrice1 + matrice2), nrow=2) ; Matricesommeligne1
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
[1,] 26 52 44 25 22 43 38 22 18 27 41 26
[2,] 48 36 30 29 24 29 34 31 33 35 35 30
matricesommeligne2 <-matrix ((matrice1 + matrice2), nrow=2, byrow=T) ; matricesommeligne2
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
[1,] 26 48 52 36 44 30 25 29 22 24 43 29
[2,] 38 34 22 31 18 33 27 35 41 35 26 30
matricetotal <-matrix (append (matrice1, matrice2), ncol=4) # Utilise “append” pour former une nouvelle matrice
matricetotal
[,1] [,2] [,3] [,4]
[1,] 13 11 13 27
[2,] 27 12 21 22
[3,] 21 ……etc
#Opérations sur les matrices
#nombre de lignes et de colonnes d’une matrice :
nrow(matricetotal); ncol(matricetotal)
[1] 12
[1] 4
# sommes par ligne et par colonne, respectivement :
rowSums(matricetotal)
[1] 64 82 74 67 62 63 52 64 63 59 69 59
colSums(matricetotal)
[1] 214 175 194 195
#moyennes par ligne et par colonne, respectivement :
rowMeans(matricetotal)
[1] 16.00 20.50 18.50 16.75 15.50 15.75 13.00 16.00 15.75 14.75 17.25 14.75
colMeans(matricetotal)
[1] 17.83333 14.58333 16.16667 16.25000
#Transposée :
t(matricetotal)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
[1,] 13 27 21 22 31 11 14 18 13 9 19 16
[2,] 11 12 11 13 9 17 15 22 24 13 13 15
[3,] 13 21 31 14 13 19 11 11 9 15 24 13
[4,] 27 22 11 18 9 16 12 13 17 22 13 15
2.4 A partir d’un fichier texte (les fichiers sont disponibles pour le téléchargement en bas de la partie 2)
Datamatricetxt<-read.table ("C:/Users/b/Desktop/Stat-R/data/matrice.txt",header = F) # Attention au chemin et au nom de fichier, le tout entre guillemets anglais. Header = F signifie qu’il n’y a pas de noms de colonnes !
#Remarque: Par défaut “header" est supposé “False”.
Datamatricetxt
1 13 11 13 27
2 27 12 21 22
3 21 11 31 11
4 22 13 14 18
5 31 9 13 9
Datamatrice1txt <-read.table ("C:/Users/b/Desktop/Stat-R/data/matrice1.txt",header = T)
Datamatrice1txt
Var1 Var2 Var3 Var4
1 13 11 13 27
2 27 12 21 22
3 21 11 31 11
4 22 13 14 18
5 31 9 13 9
# S’ils n’existent pas, les titres des colonnes peuvent être créés avec l’option col.names
Datamatricenc<-read.table ("C:/Users/b/Desktop/Stat-R/data/matrice.txt", col.names = c("Variable1","Variable2","Variable3","Variable4"))
Datamatricenc
Variable1 Variable2 Variable3 Variable4
1 13 11 13 27
2 27 …..etc
2.5 A partir d’un fichier Excel :
#Enregistrer le fichier “Excel” au format .csv (séparateur = point-virgule).
#Par défaut, “header" est supposé “True”. Le préciser si ce n’est pas le cas !
DataExcel<-read.csv2("dataexcel.csv")
DataExcel
Variable1 Variable2 Variable3 Variable4
1 13 11 13 27
2 27 12 21 22
3 21 11 31 11
4 22 13 14 18
5 31 …..etc
install.packages("readxl")
library(readxl)
dataExcel <- read_excel("Flamants.xlsx", 1) # Ouvrir la feuille n°1 du fichier Excel (.xlsx)
dataExcel
# A tibble: 52 x 4
Aile Tarse Masse Sexe
<dbl> <dbl> <dbl> <chr>
1 290 233 2270 F
2 254 206 1850 F
3 263 222 2200 F
# ... with 42 more rows
dataExcel1 <- read_excel("Flamants.xlsx", sheet = 3) # Ouvrir la feuille n°2 du fichier Excel (.xlsx)
dataExcel1
# A tibble: 6 x 3
Year Breeding Pairs
<dbl> <chr> <dbl>
1 2006 yes 4700
2 2007 no 0
3 2008 no 0
dataExcel2 <- read_excel("Flamants.xlsx", sheet = "Flamants") # Ouvrir la feuille n°2 du fichier Excel (.xlsx)
dataExcel2
# A tibble: 52 x 4
Aile Tarse Masse Sexe
<dbl> <dbl> <dbl> <chr>
1 290 233 2270 F
2 254 206 1850 F
3 263 222 2200 F
# ... with 42 more rows