Notions de base de la MDF
Dans cette section on va revoir les principales notions de la mécanique des fluides que nous allons rencontrer tout le long des prochains chapitres.
Principe fondamental de l'hydrostatique: qui s'intéresse aux fluides au repos (immobiles)
(1)
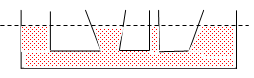
Comme nous pouvons le constater il y' a un lien entre la pression et la hauteur du liquide par la relation (1)
Le débit volumique: est le volume d'un liquide traversant une section droite par unité de temps
Le débit massique: c'est le produit du débit volumétrique par la masse volumique (ρ) du liquide considéré.
Equation de continuité:
- conservation de la masse
En régime permanent on va avoir conservation du débit massique du liquide qui circule à l'intérieur de la conduite,
si le fluide est incompressible ça veut dire que la masse volumique est constante donc:
où:
v: vitesse du liquide à l'intérieur de la conduite [m/s]
s: section du passage à l'intérieur de la conduite:
ρ : masse volumique du fluide considéré [kg/m3]
Equation de BERNOULLI pour les fluides en mouvement
- Equation de BERNOULLI pour un fluide parfait incompressible sans échange de travail, c'est-à-dire que sa viscosité est nulle et sa masse volumique est constante
comme nous pouvons le constater que la somme des trois termes (l'énergie de pression, l'énergie potentielle et l'énergie cinétique) est constante,
l'équation de BERNOULLI traduit la conservation de l'énergie.
d'après cette équation on peut voir aussi qu'on va pouvoir transformer une forme d'énergie en autre forme par exemple si on augmente le diamètre de la conduite en gardant la meme hauteur (Z) donc l'énergie potentielle reste constante, on aura une perte d'énergie cinétique et une augmentation de la pression.
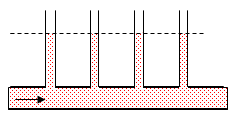
Ecoulement d'un fluide parfait dans une conduite
Si on a un liquide parfait incompressible qui circule à l'intérieur d'une conduite horizontale de diamètre constant la pression reste constante.
Equation de BERNOULLI pour un liquide réel incompressible. En réalité un fluide parfait n'existe pas dans la nature donc les fluides ont une viscosité. Si on écrit l'équation de BERNOULLI entre deux points 1 et 2 d'un tronçon de conduite on aura les memes termes que l'équation précédente plus un autre terme qui exprime la perte d'énergie entre les deux points qu'on appelle aussi pertes de charge
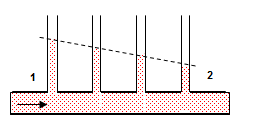
Ecoulement d'un fluide réel dans une conduite
Nous pouvons constater que le niveau de pression diminue au fur et à mesure qu'on avance dans cette conduite cette dimunition est due à cette perte de charge
l'équation de BERNOULLI peut se présenter sous trois formes
a) En pression [pa]
b) En colonne de fluide
c) En joule par Kilogramme.
Les pertes de charges: Les pertes de charge sont dues aux frottements visqueux entre les couches du fluide d'une part et des frottements du liquide contre les parois de la conduite d'autre part, ainsi que les changements des formes et dimension des obstacles que rencontre le fluide au cours de son déplacement (composants hydrauliques, coudes etc). Ces pertes se présentent sous deux types:
- Pertes de charge linéaire ou réparties
- Pertes de charge locales ou singulières
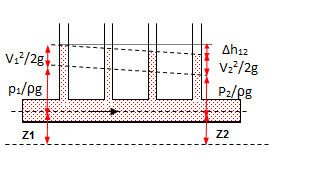
: est la somme des pertes de charge totale entre le point 1 et 2
a) Pertes de charge linéaire: Les pertes de charge linéaire dépendent des dimensions de la conduite (longueur et diamètre) de la viscosité du fluide et de la vitesse de son écoulement.
La perte de charge linéaire est déterminée par la relation suivante:
où:
- λ: Coefficient de perte de charge linéaire qui dépend du régime d'écoulement du liquide
- L; Longueur de la conduite [m]
- D: Diamètre de la conduite [m]
- v: Vitesse moyenne du liquide à l'intérieur de la conduite [m/s]
La perte de charge locale est déterminée par la relation suivante:
Ou: ξ est le coefficient de perte de charge locale, il dépend de la forme et des dimensions de l'obstacle; on peut les trouver sous forme de tableaux ou courbes donnes par les constructeurs des composants.
La viscosité:
La viscosité est la caractéristique d’un fluide qui définit sa résistance à l’écoulement.
Sous l'effet des forces d'interaction entre les molécules de fluide et des forces d'interaction entre les molécules de fluide et celles de la paroi, chaque molécule de fluide ne s'écoule pas à la même vitesse.
La vitesse de chaque couche est une fonction de la distance( y) de cette courbe au plan fixe, on dit qu'il existe un profil de vitesse.
Le mouvement du fluide peut être considéré comme résultant du glissement des couches de fluide les unes sur les autres
Plusieurs grandeurs physiques la déterminent , parmi lesquelles la viscosité dynamique et la cinématique.
- La viscosité dynamique
Deux couches de fluide circulent parallèlement à des vitesses différentes. La force de frottement que chacune exerce l’une sur l’autre est:
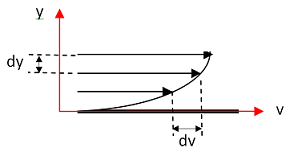
Où;
τ: Contrainte tangentielle [N/m2]
μ : Le facteur de proportionnalité est le coefficient de viscosité dynamique du fluide
S: surface commune aux deux lames [m²]
Dans le système international (SI), l'unité de viscosité est le:
[Pa.s] ou Poiseuille (Pl): 1[Pl] = 1 [kg/m.s]
On trouve encore les tables de valeurs numériques le coefficient de viscosité dans un ancien système d'unités (CGS): L'unité est le Poise (Po); 1 [Pl] = 10 [Po] = 1 [daPo] = 103 [cPo]
- La viscosité cinématique
La viscosité cinématique est le rapport de la viscosité dynamique et la masse volumique du liquide considéré.
Unité: Dans le système international (SI), l'unité de viscosité n'a pas de nom particulier : [m2/s]. Dans le système CGS, l'unité est le Stoke (St) : 1 [m2/s] = 104 [St].
La viscosité engendre un gradient de vitesse dans une section droite de conduite :
- à la paroi, la vitesse du fluide est nulle (c'est la condition d'adhérence) ;
- la vitesse est maximale au centre de la conduite.
La figure ci-dessous montre les différents types de profils rencontrés en fonction du type de fluide et du régime d'écoulement.
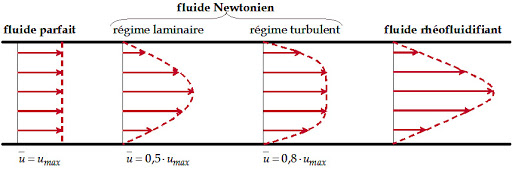
Paramètres physiques influant sur la viscosité
a) La température
L’augmentation de la température d’une huile a pour effet de diminuer sa viscosité (et inversement). La valeur de cette variation peut être donnée par des abaques (exemple ci-dessous) ou par l’indice de viscosité.
L’augmentation de la température d’une huile a pour effet de diminuer sa viscosité (et inversement). La valeur de cette variation peut être donnée par des abaques (exemple ci-dessous) ou par l’indice de viscosité.
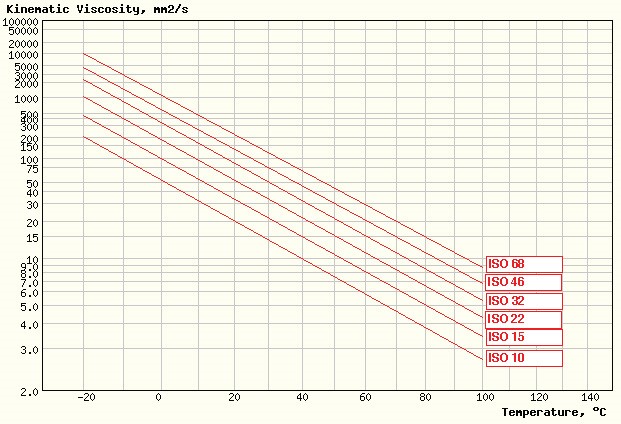
La variation de la viscosité en fonction de la température
b) La pression
la viscosité des liquides augmente avec l'augmentation de le pression, aux environs des 300 bars elle peut doubler; la viscosité d'un liquide à une pression donnée (ν(p)) peut etre déterminée par l"expression suivante:
où:
- ν(p) : la viscosité à la pression (p)
- ν(0) : la viscosité à la pression atmosphérique
- a: Coefficient propre à l'huile utilisée pour les huiles minérales a=0.002
- p: pression de service
- Les régimes d'écoulement
La connaissance du régime d'écoulement est indispensable pour la détermination du coefficient de pertes de charge linéaire.
Le régime d'écoulement dépend du débit, du diamètre de la conduite et les propriétés du fluide. Reynolds a défini trois grands régimes d'écoulement défini comme suit dans le cas d'un écoulement dans une conduite cylindrique :
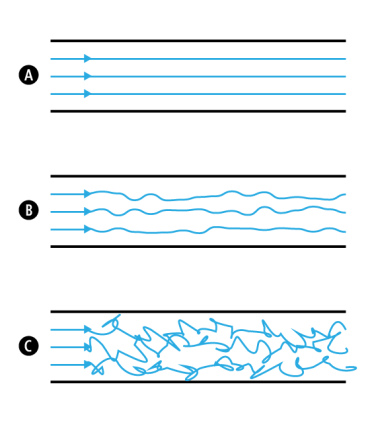
- L'écoulement laminaire : écoulement rectiligne, le fluide s'écoule en filets parallèles à l'axe de la conduite, sans mélange. figure (A)
- L'écoulement intermédiaire : l'écoulement est plus ou moins rectiligne, avec un peu de mélange (petits tourbillons). Figure (B)
- L'écoulement turbulent : l'écoulement se fait avec de grands tourbillons, avec un mélange important.Figure (C)
Où:
- Re : nombre de Reynolds (sans dimension)
- ρ: masse volumique du fluide (kg.m-3)
- vm : vitesse moyenne du fluide (m/s)
- D diamètre de la conduite (m)
- μ: viscosité dynamique du fluide (Pa.s)
- ν: viscosité cinématique du fluide (m2 /s)
Pour Re≤2300, l'écoulement est laminaire.
Pour 2300 ≤ Re≤3000 l'écoulement est transitoire (ça varie d'un auteur à un autre mais comprise entre 3000 et 10000.
Turbulent
- Pour 2300≤Re≤105, l'écoulement turbulent lisse.
- Pour Re>105, l'écoulement est turbulent rugueux.
Détermination du coefficient de pertes de charge linéaire
Si le régime d'écoulement est laminaire
Si le régime d'écoulement est turbulent lisse:
Si le régime d'écoulement est turbulent rugueux dans ce cas l'état de surface interne de la conduite
Où :
ε: est la rugosité de la surface interne de la conduite
Equation de BERNOULLI avec échange de travail:
Lorsque le fluide traverse une machine hydraulique, il échange de l’énergie avec cette machine sous forme de travail (dW) pendant une durée (dt). La puissance P échangée est
Unités : P en watt (W), W en joule (J), t en seconde (s).
- P > 0 si l’énergie est reçue par le fluide (ex. : pompe) ;
- P< 0 si l’énergie est fournie par le fluide (ex. : turbine).
- P=0 si il n' y a aucune machine entre le point 1 et 2
Si le débit-volume est qv, la relation de Bernoulli s’écrit alors :
Ou:
∑P : somme des puissances échangées entre le fluide et le milieu extérieur, à travers une machine, entre (1) et (2)
Δp: la somme des pertes de charge entre les points 1 et 2, qui sont dues aux frottements du fluide sur les parois de la conduites et les obstacles (résistances hydrauliques)